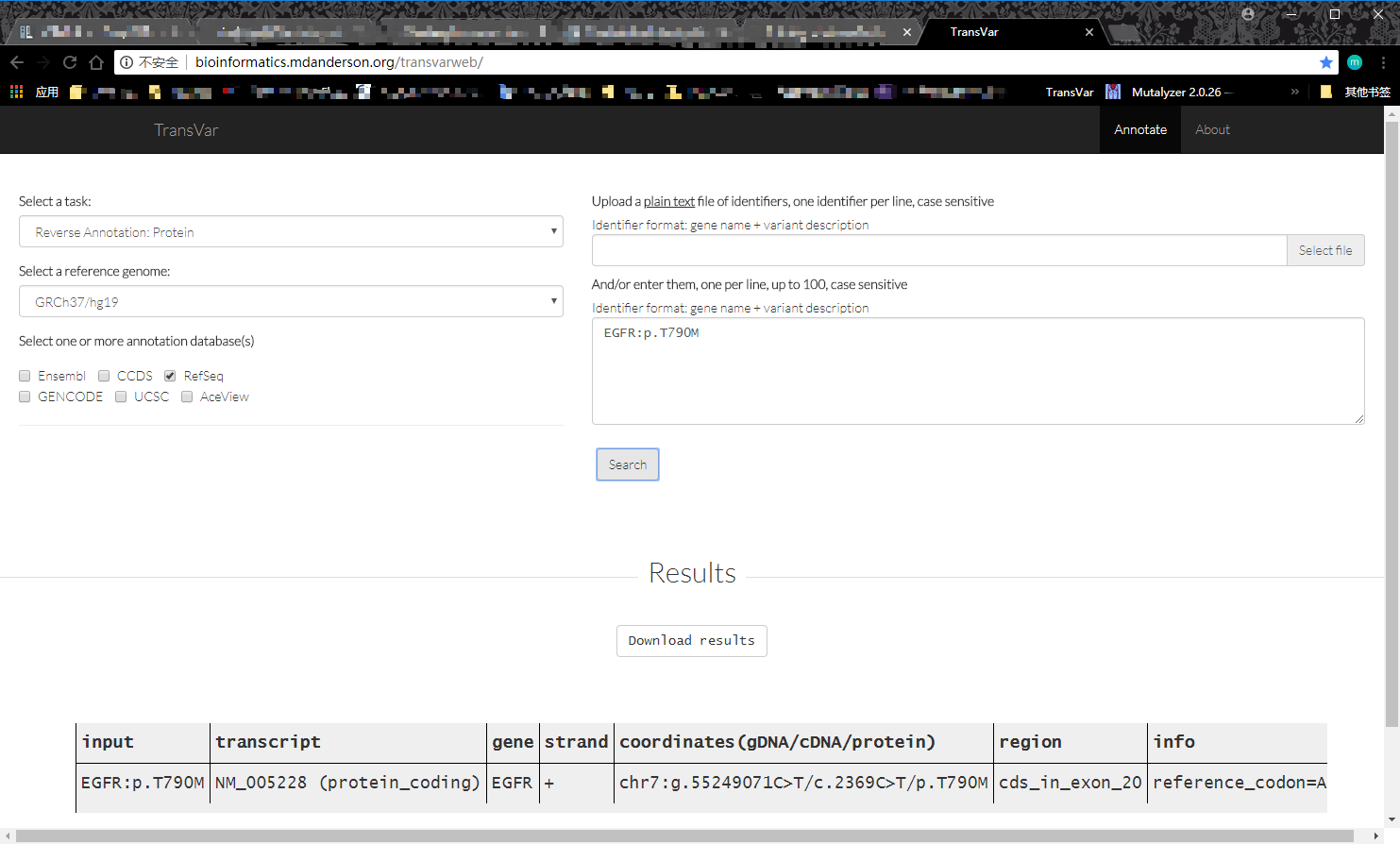
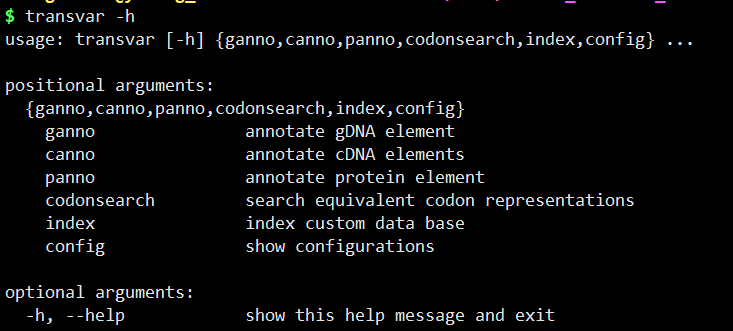
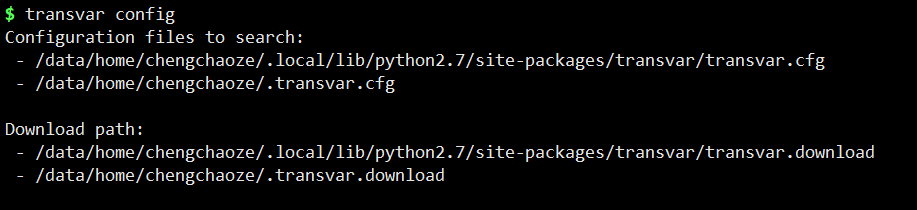
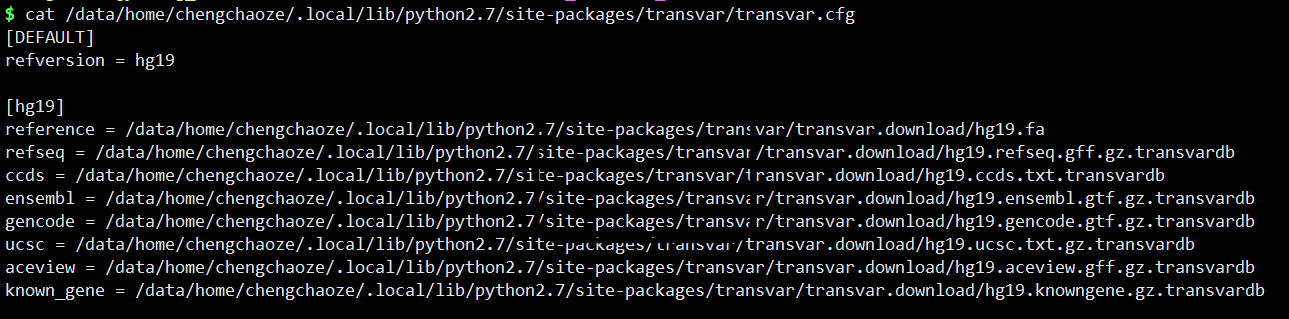
KNN 是一种分类和回归算法,利用训练集数据计算特征向量空间距离,根据距离最近的 k 个训练实例,根据分类决策规则对输入实例进行分类,算法不具备显示的学习过程。knn 算法三个基本要素为距离算法、k值选择、分类决策规则
距离算法
空间中两个实例点之间的距离,可反应两个实例点之间的相似程度。通常计算为闵氏距离(Minkowski distance),如下:
$$L_{p}(x_i, x_y) = {(\sum_{l=1}^n |x_i^{(l)} - x_J^{(l)}|^p)}^\frac{1}{p}$$
p==1时,即为曼哈顿距离(Manhattan Distance):
$$L_1(x_i, x_j) = \sum_{l=1}^n |x_i^{(l)} - x_J^{(l)}|$$
p==2 时,即为欧式距离(Euclidean Distance):
$$L_2(x_i, x_j) = {(\sum_{l=1}^n |x_i^{(l)} - x_J^{(l)}|^2)}^\frac{1}{2}$$
p = $\infty$ 时,即为切比雪夫距离(Chebyshev distance)
$$L_{\infty}(x_i, x_y) = \lim_{p \to \infty} {(\sum_{l=1}^n |x_i^{(l)} - x_J^{(l)}|^p)}^\frac{1}{p} = max_l(|x_i^{(l)} - x_J^{(l)}|)$$
K值选择
- K 值小,近似误差减少,估计误差增大,模型复杂。预测结果对邻近的实例敏感,容易受极端值影响
- K 值大,估计误差减小,近似误差增大,模型简单。假设 K 等于训练集 N,预测结果始终属于训练集中最多的类。
- 一般选取较小的 K 值,交叉验证选取最优 k 值
决策规则
- knn 的分类规则一般时多数表决,即由实例的 k 个相邻训练实例中的多数决定